vague – IUEM

Archive d’étiquettes pour : vague

Mesurer les courants depuis l’espace, un défi houleux

Grâce à un nouveau projet de satellite, les océanographes espèrent obtenir pour la première fois une mesure directe des courants marins de surface depuis l’espace. Cette prouesse technique passe par une connaissance précise de la géométrie des vagues.

Obtenir une mesure des courants marins de surface est l’un des défis essentiels de l’Océanographie. Au-delà des applications civiles et industrielles (pour la navigation, la construction off-shore …etc.), la connaissance de ces courants est au cœur de nombreux enjeux scientifiques car les différents échanges Atmosphère – Océan (de chaleur, de carbone, etc…) s’opèrent en surface et dépendent de ces courants.

Figure 1 : Exemple de courants de surface obtenus à partir d’un modèle numérique. Les panneaux de droite “zooment” vers les 2 régions encadrées en violet (à gauche)

Or les modèles numériques théoriques montrent qu’il existe une multitude de courants, organisés sous forme de structures de tailles variables (cf. fig. 1 : courants issus d’un modèle théorique où coexistent des courants visibles à l’échelle du globe (en turquoise clair, image de gauche) et des courants d’une échelle plus petite (en rouge, image de droite).

Mais l’origine et l’évolution de ces courants restent mal comprises car les mesures directes, qui pourraient permettre une comparaison avec les calculs théoriques, ne sont pas suffisantes. Elles sont en effet effectuées soit par des radars au sol à portée limitée, soit par des bouées ou des instruments océanographiques qui dérivent en surface et réalisent des mesures ponctuelles ne permettant pas d’obtenir une représentation globale à l’échelle océanique. Les mesures satellitaires pourraient, quant à elles, fournir une telle représentation des courants, mais les satellites actuels (des altimètres) ne les mesurent pas directement, ils se contentent de les évaluer via les variations de hauteur de la surface de l’océan.

Pour estimer les courants de surface à partir de ces données altimétriques, il est nécessaire que la taille et la vitesse des courants satisfassent certaines hypothèses. Malheureusement celles-ci ne sont pas entièrement vérifiées lorsqu’il s’agit de courants de petite échelle et/ou de forte intensité pour lesquels l’erreur d’estimation demeure très importante quand leur évaluation est réalisée à partir des mesures de hauteur de surface de l’océan. Par ailleurs, à proximité de l’équateur, l’estimation des courants s’avère de mauvaise qualité et rend de ce fait les mesures par altimètres très difficiles à pratiquer, dans cette zone géographique. Ces satellites apparaissent donc plus aptes à apprécier les courants de grande échelle et d’intensité faible, à distance de l’équateur.

Récemment, un nouveau concept permettant une mesure directe des courants (sans estimation) a été proposé : le SKIM (Sea surface KInematics Multiscale monitoring concept). Il s’agit d’une mesure de l’effet Doppler produit par la surface de l’océan, effectuée depuis l’espace.

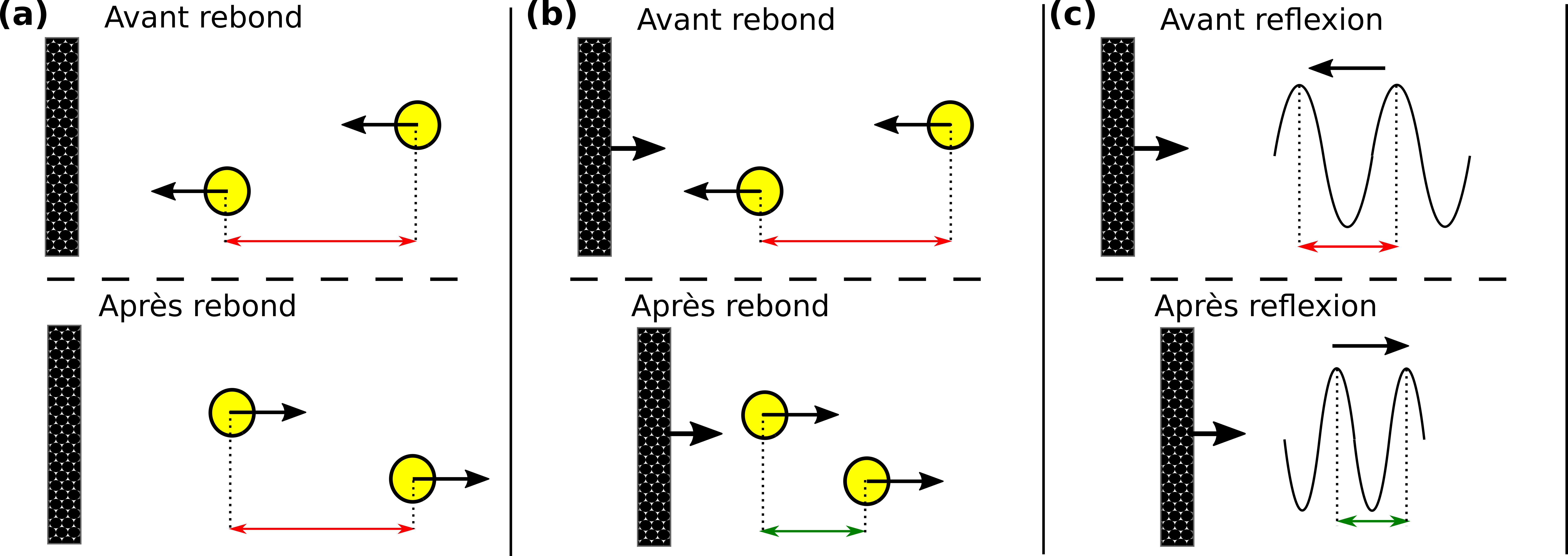
Figure 2: Schéma explicatif de l’effet Doppler

Qu’est-ce que l’effet Doppler?

Quand deux balles sont lancées horizontalement à la même vitesse, contre un mur et que la deuxième balle est lancée quelques secondes après la première (fig. 2a), la distance entre les balles reste constante, même après un rebond contre le mur (cf. fig. 2a : flèches rouges). Si le mur avance vers le lanceur (cf. fig. 2b), une fois que la première balle a rebondi, le mur continue d’avancer vers la deuxième balle, ainsi elle rebondit plus tôt que si le mur était resté fixe et donc elle change de direction plus rapidement que prévu. Par conséquent, si l’on mesure la distance séparant les deux balles après le rebond, celle-ci est plus courte qu’avant le rebond (cf. fig. 2b : flèche verte).

Cette diminution de la distance entre les deux balles, due au déplacement de l’obstacle, est le fondement de l’effet Doppler observé pour des ondes électromagnétiques. Une onde électromagnétique peut être considérée comme une succession de crêtes et de creux dans le champ électromagnétique (cf. fig. 2c). Les deux balles représentent deux crêtes successives de l’onde. A l’émission de l’onde, les crêtes sont séparées par une certaine distance (la longueur d’onde, cf. fig. 2c : flèche rouge). Mais après réflexion contre un mur qui se déplace, la distance entre ces deux crêtes change, la longueur d’onde a donc changé (cf. fig. 2c : flèche verte). En mesurant ce changement (l’effet Doppler), on peut estimer la vitesse de déplacement du mur.

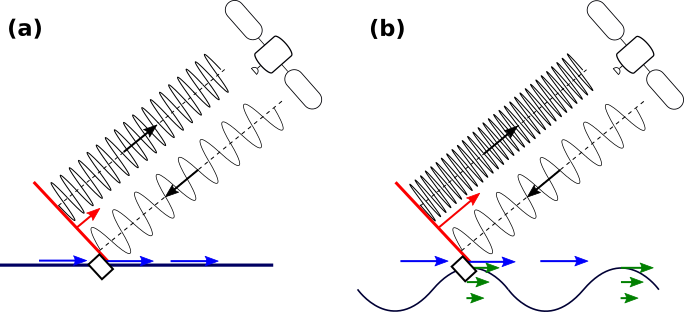
Figure 3 : Principe de mesure des courants par satellite grâce au concept SKIM

Le principe de SKIM est de réaliser une mesure de la vitesse de la surface de l’océan par effet Doppler. Pour cela, le futur satellite devra émettre une onde électromagnétique à un certain angle par rapport à la verticale. Si (cf. fig. 3a) la surface de l’océan est globalement plate, avec un élément flottant (petit rectangle noir : le réflecteur), l’onde va être réfléchie sur cet élément et être en partie réémise en direction du satellite, de la même manière que si un mur (cf. fig.3a : en rouge) était présent. S’il existe un courant en surface (cf. fig.3a : flèches bleues), celui ci va faire bouger le réflecteur et le «mur» va se déplacer. Il se produit alors un effet Doppler qui permet d’estimer la vitesse de déplacement du réflecteur et par conséquent du courant qui le déplace.

Quel est le rôle des vagues dans cette mesure des courants ? (cf. fig. 3b)

Si l’océan n’est pas plat mais que des vagues modifient significativement la géométrie de sa surface, celles-ci génèrent un courant faible dans le sens de leur propagation (appelé la dérive de Stokes) qui déplace le réflecteur. Le courant mesuré par effet Doppler correspondra donc à la somme du courant marin de surface (que l’on cherche à mesurer – cf. fig. 3b : flèches bleues) et de cette dérive de Stokes due aux vagues (cf. fig. 3b : flèches vertes). Pour évaluer le courant de surface, une connaissance précise de la dérive de Stokes et des vagues sont donc nécessaires. Cette estimation des vagues constitue ainsi la deuxième action à effectuer nécessairement par le futur satellite, via d’autres propriétés liées à l’onde électromagnétique émise.
Ce nouveau concept SKIM pourrait donc permettre de mesurer par effet Doppler, les courants marins de surface depuis l’espace, avec une haute résolution spatiale (de l’ordre de 30 km) et temporelle (de l’ordre d’1 mesure tous les 3 jours) pour l’ensemble du globe et plus spécifiquement à proximité de l’équateur. La mesure simultanée des vagues, serait nécessaire afin d’estimer le courant qu’elles induisent et ainsi de pouvoir le soustraire au signal mesuré.

Malgré un concept relativement simple, la mise en œuvre de SKIM reste un formidable défi scientifique du fait de la multiplicité et de la complexité des sources d’erreurs potentielles. En effet, si le satellite se déplace à 7 kilomètres/seconde, les courants ont quant à eux des vitesses inférieures à un mètre/seconde, il est donc essentiel que l’emplacement et la vitesse du satellite soient connus avec une grande précision pour que la mesure du courant puisse s’avérer tout à fait fiable.

Médiation scientifique

Assurée par Alex Ayet, l‘École Doctorale des Sciences de la Mer et du Littora l (EDSML – Université Bretagne – Loire), en 3ème année de thèse dans l’équipe SIAM au sein du laboratoire d’océanographie physique et spatiale (LOPS) à l’Ifremer.

L’article

Measuring currents, ice drift, and waves from space: the Sea surface KInematics Multiscale monitoring (SKIM) concept https://doi.org/10.5194/os-14-337-2018

Les auteurs

Ce travail résulte d’une collaboration internationale entre Fabrice Ardhuin, Bertrand Chapron, Jean-Marc Delouis, Alexis Mouche, Frédéric Nouguier et Justin Stopa (Laboratoire d’Océanographie Physique et Spatiale (LOPS), Univ. Brest, CNRS, Ifremer, IRD, Brest, France), Yevgueny Aksenov et George Nurser (National Oceanographic Center, Southampton, Angleterre), Alvise Benetazzo (Institute of Marine Sciences, National Research Council (ISMAR-CNR), Venice, Italie), Laurent Bertino, Johnny Johannessen, Anton Korosov, Pierre Rampal et Jiping Xie (Nansen Environmental and Remote Sensing Center, Bergen, Norvège), Eric Caubet (Thales Alenia Space, Toulouse, France), Fabrice Collard et Lucile Gaultier (OceanDataLab, Locmaria Plouzané, France), Sophie Cravatte (LEGOS, Université de Toulouse, CNES, CNRS, IRD, Toulouse, France), Frederic Dias (University College, Dublin, Irlande), Gérald Dibarboure et Céline Tison (CNES, Toulouse, France), Georgy Manucharyan (Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, Etats-Unis), Dimitris Menemenlis et Ernesto Rodriguez (Earth Sciences Division, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, Etats-Unis), Melisa Menendez (Environmental Hydraulics Institute “IH Cantabria” Universidad de Cantabria, Santander, Espagne), Goulven Monnier (Scalian Alyotech, Rennes, France), Ad Reniers et Clément Ubelmann (Collecte Localisation Satellite (CLS), Ramonville St-Agne, France) et Erik van Sebille (Institute for Marine and Atmospheric Research, Utrecht University, Utrecht, Pays-Bas).

La revue

“Ocean sciences” est une revue en Open-Access publiée par l’European Geophysical Union. Elle traite de tous les aspects de l’océanographie physique, qu’il s’agisse d’études expérimentales, théoriques ou en laboratoire.

Contacts

Auteurs : consulter l’annuaire de l’IUEM

Bibliothèque La Pérouse : Suivi éditorial, rédaction, corrections et mise en page : Fanny Barbier

Service Communication et médiation scientifique : communication.iuem@univ-brest.fr

5 novembre 2019/par cyven

Mesurer la glace ? pas de quoi en faire des vagues

Actualité archive

La fonte inéluctable des glaces de mer rend nécessaire d’en estimer l’épaisseur. C’est possible, il suffit pour cela de mesurer les vagues…

La couverture de glace au niveau des pôles a beaucoup diminué depuis 1979, année des premières observations satellitaires, le réchauffement direct de notre atmosphère et les différents phénomènes physiques associés (modification des courants, intensification des événements climatiques extrêmes…) en sont les principaux responsables. Ainsi dans les régions polaires, les interactions entre les vagues et la glace sont de plus en plus importantes. En Arctique, l’étendue des glaces ayant considérablement diminué, la surface d’océan en eau libre a augmenté permettant aux vagues de se déployer. En Antarctique, les vagues ont un effet stabilisateur, elles viennent compresser la glace et lui opposent ainsi une résistance à l’éloignement vers l’équateur et des eaux plus chaudes où elle fondrait.

Quand les vagues arrivent à hauteur d’un objet flottant, il les réfléchit et/ou les amortit, tout comme la quantité de mouvement qu’elles transportent. Cela produit une force horizontale sur l’objet (ici la glace de mer) qui peut amener son déplacement ou sa déformation. La compression entraîne l’épaississement des couches de glace flottantes sous forme d’empilements verticaux des morceaux de glace présents dans la zone de transition entre l’océan et la banquise (cf. fig. 1), c’est la Zone Marginale de Glace (ZMG). Les morceaux de glace, formant initialement une seule couche morcelée à la surface de la mer, peuvent se retrouver compressés jusqu’à se soulever pour s’empiler sur d’autres. C’est le mouvement incessant des vagues qui favorise ce soulèvement en modifiant constamment les espacements et hauteurs des glaces flottantes. A partir d’un certain point, la force exercée par les vagues devient insuffisante pour compresser d’avantage la glace qui arrête alors d’épaissir.

L’étude présentée ici s’appuie sur la capacité de calculer la variation du mouvement de la glace à la surface de l’océan lorsqu’elle est soumise aux contraintes qui s’opposent à sa déformation : les contraintes externes sur la glace (les vagues, le vent, les courants) et la contrainte interne à la glace. Prenons l’exemple d’une boule de neige : la contrainte externe lui est imposée par nos mains qui tassent la neige tandis que la résistance de la neige au tassement, constitue la contrainte interne. L’opposition de ces deux contraintes, permet d’obtenir une boule de neige compacte, de taille constante pour une quantité de neige donnée.

Fig. 1 : Agrégation et compactage des morceaux de glace par les vagues (provenant de la gauche) vers la banquise (à droite)

Lorsque la glace ne bouge plus, on dit que le système glace-océan-atmosphère est à l’équilibre. Les contraintes externes et internes s’égalisent (la boule de neige est constituée et ne se tasse plus). Connaître la valeur de l’une des deux contraintes, c’est connaître la valeur de l’autre, on peut donc estimer les contraintes internes par des mesures extérieures (via un satellite par ex.), or comme on sait relier mathématiquement les contraintes internes à l’épaisseur de la glace, on peut alors déterminer celle-ci à partir de mesures océanographiques !

Des expériences ont ainsi été réalisées dans le parc national du Bic, véritable laboratoire naturel au long de l’estuaire du fleuve Saint-Laurent (Canada). Durant l’hiver et malgré une couverture de glace presque totale, une partie du fleuve reste cependant libre de glace par l’apport en eaux plus chaudes, provenant de l’océan Atlantique. Lors d’épisodes venteux, des vagues s’y forment (ce serait impossible si toute la surface du fleuve était gelée) permettant ainsi l’étude d’une ZMG. Des mesures comparatives de courant, de vent et d’épaisseur de glace ont donc pu y être effectuées. Des bouées équipées de capteurs de mouvements et placées en différents points toujours plus éloignés du bord, ont permis d’effectuer des mesures de vagues (cf. fig. 2a) ; ce positionnement permet d’évaluer l’atténuation progressive des vagues par la glace. On observe ainsi (cf. fig. 2b) que l’énergie des vagues, mesurée pour chaque bouée, diminue à mesure qu’on s’éloigne de la zone d’eau à l’air libre, en suivant une loi de décroissance exponentielle.

En pratique, cette atténuation peut être ici associée à trois phénomènes : la réflexion des vagues sur la glace et vers le large, la dissipation de l’énergie des vagues par la turbulence (remous occasionnés par la rencontre entre les vagues et la glace) ou encore la friction entre morceaux de glace. Le premier phénomène reste négligeable car les morceaux de glaces sont de petites tailles vis-à-vis de la longueur des vagues (ce n’est pas toujours le cas). Le second n’a pas pu être mesuré durant les missions de terrain (mais compte tenu d’autres observations, il peut ne pas être négligeable). Ainsi, si l’atténuation examinée ici tient compte uniquement de la friction des glaces (troisième phénomène), il faut souligner que le résultat final est probablement sous-évalué, car l’effet de turbulence n’a pas été pris en considération.

Fig. 2a : Zone d’étude avec le parcours réalisé par les bouées lors d’une des séries de mesures. L’échelle de couleur indique le temps associé à la position de chaque bouée.

Fig. 2b : Atténuation de l’énergie E des vagues en fonction de la distance X_ice au bord de glace. Plus la couleur est foncée, plus la bouée considérée se situe loin du bord.

Les mesures d’épaisseur ont été réalisées via des trous percés dans la glace, on y a introduit un bâton terminé d’un crochet afin de ne pas dépasser la surface inférieure du glaçon. Les mesures de vent et de courant ont montré que leur effet sur la glace reste négligeable comparé à celui des vagues. De ce fait, la mesure de l’atténuation des vagues permet directement d’estimer l’évolution de la contrainte externe des vagues sur la glace et celle de l’épaisseur de glace en fonction de la distance au bord de glace (cf. fig. 3). Cette épaisseur croît rapidement jusqu’à atteindre une valeur maximale constante, concomitante à la disparition totale des vagues. La modélisation de l’évolution d’épaisseur de la glace correspond bien aux mesures effectuées sur le terrain. La disparité des mesures individuelles est due à la forte variabilité de l’état de surface de la glace.

Fig. 3 : Evolution de l’épaisseur de glace ζ divisée par l’épaisseur de glace à l’équilibre ζ_eq en fonction de la distance au bord de glace χ. La ligne noire désigne le modèle mathématique, les ronds les mesures par bouée, les croix les mesures directes de l’épaisseur, les carrés et le losange jaunes les moyennes des croix.

Ces résultats sont encourageants pour la communauté scientifique. En effet contrairement aux mesures des vagues observées toujours plus précisément via les données satellitaires, les estimations d’épaisseur de glace restent très difficiles à réaliser dans des conditions identiques. Grâce à cette découverte, l’estimation par satellite de l’épaisseur des glaces à partir des mesures de vagues devient envisageable (au moins dans des conditions similaires à celles présentées dans cette étude).

Médiation scientifique:

Assurée par Luc Barast, doctorant de l‘École Doctorale des Sciences de la Mer et du Littora l (EDSML – Université Bretagne – Loire), en 1ère année de thèse dans l’équipe SIAM au sein du Laboratoire d’Océanographie Physique et Spatiale (LOPS) à l’Ifremer.

L’article

Marginal ice zone thickness and extent due to wave radiation stress.

https://doi.org/10.1175/JPO-D-17-0167.1

Les auteurs

Ce travail résulte d’une collaboration entre Peter Sutherland, (Ifremer, Univ. Brest, CNRS, IRD, Laboratoire d’Océanographie Physique et Spatiale, IUEM, Brest, France) et Dany Dumont (Institut des Sciences de la Mer de Rimouski, Université du Québec à Rimouski, Rimouski, Quebec, Canada) autour du projet BicWin, à propos de l’étude des phénomènes physiques et océanographiques des ZMG à partir du laboratoire naturel que constitue le parc du Bic.

La revue

« Journal of Physical Oceanography » est une revue publiée par l’American Meteorological Society. Elle traite de la physique des océans et des processus ayant lieux à leurs frontières. Les articles qui y sont publiés sont tout aussi bien basés sur de la théorie, des mesures de terrain ou par satellite, ou encore sur des résultats numériques.