New guidelines for the application of Stokes’ models to the sinking velocity of marine aggregates

Numerical simulations of ocean biogeochemical cycles need to adequately represent particle sinking velocities (SV). For decades, Stokes’ Law estimating particle SV from density and size has been widely used. But while Stokes’ Law holds for small, smooth, and rigid spheres settling at low Reynolds number, it fails when applied to marine aggregates complex in shape, structure, and composition. Minerals and zooplankton can alter phytoplankton aggregates in ways that change their SV, potentially improving the applicability of Stokes’ models. Using rolling cylinders, we experimentally produced diatom aggregates in the presence and absence of minerals and/or microzooplankton. Minerals and to a lesser extent microzooplankton decreased aggregate size and roughness and increased their sphericity and compactness. Stokes’ Law parameterized with a fractal porosity modeled adequately size‐SV relationships for mineral‐loaded aggregates. Phytoplankton‐only aggregates and those exposed to microzooplankton followed the general Navier‐Stokes drag equation suggesting an indiscernible effect of microzooplankton and a drag coefficient too complex to be calculated with a Stokes’ assumption. We compared our results with a larger data set of ballasted and nonballasted marine aggregates. This confirmed that the size‐SV relationships for ballasted aggregates can be simulated by Stokes’ models with an adequate fractal porosity parameterization. Given the importance of mineral ballasting in the ocean, our findings could ease biogeochemical model parameterization for a significant pool of particles in the ocean and especially in the mesopelagic zone where the particulate organic matter : mineral ratio decreases. Our results also reinforce the importance of accounting for porosity as a decisive predictor of marine aggregate SV.

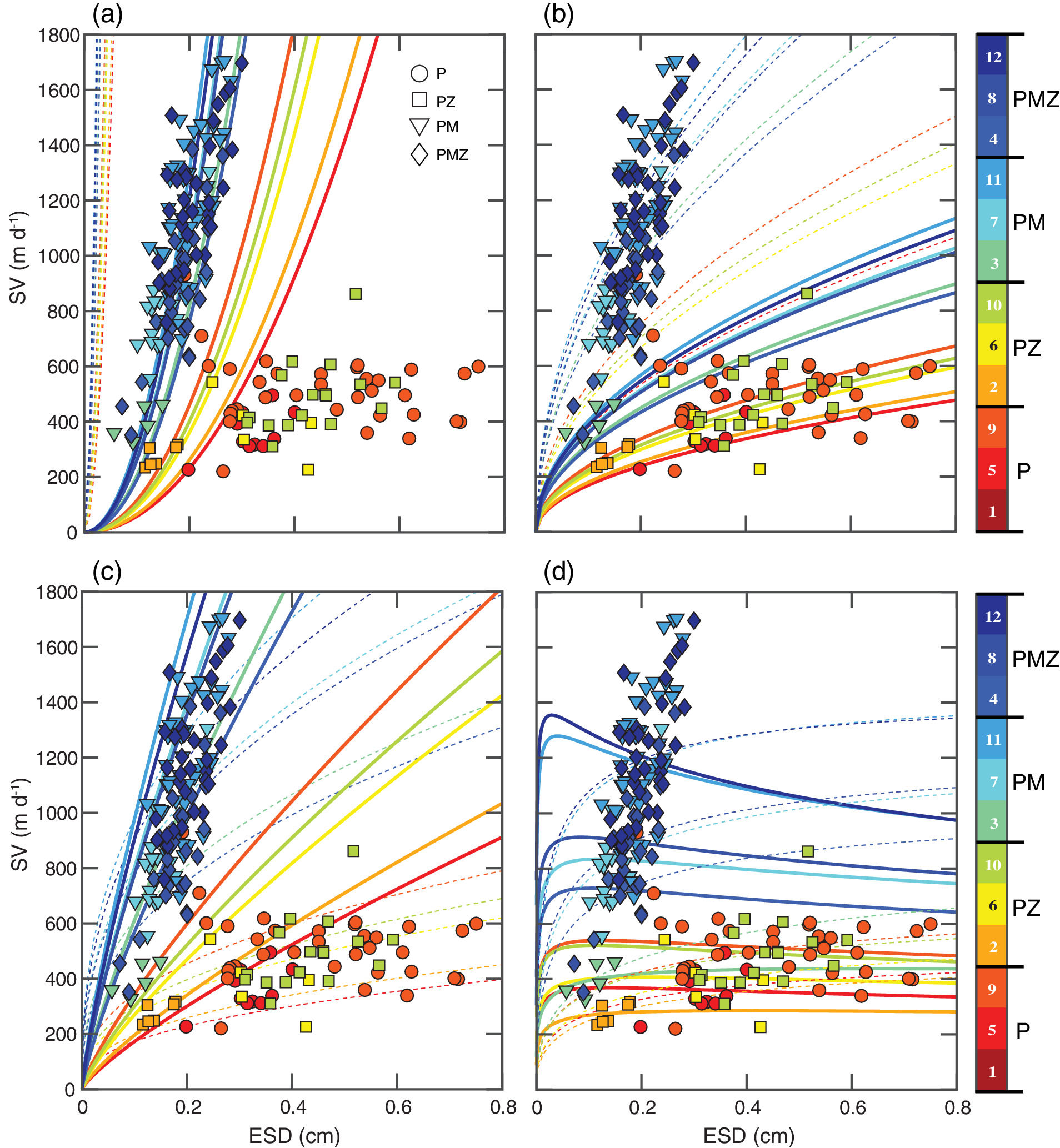
Sinking velocities vs. ESD (equivalent spherical diameter) for aggregates formed in each tank of the four treatments and comparison with theoretical expectations from different parameterizations of Stokes’ Law and the general Navier‐Stokes’ drag equation. P: phytoplankton; PZ: phytoplankton + microzooplankton (rotifers); PM: phytoplankton + mineral (calcite); PMZ: phytoplankton + mineral + microzooplankton. (a) Model 1, Stokes’ Law with constant porosities of 0% (dashed lines) and 99% (solid lines). (b) Model 2, general Navier‐Stokes’ drag law with constant drags of 1 (dashed lines) and 5 (solid lines), and a constant porosity of 99%. (c) Model 3, Stokes’ Law with a porosity scaled on a fractal geometry with coefficient a = 0.03 and D₃ = 1.4 (dashed lines) and D₃ = 1.8 (solid lines). (d) Model 4, general Navier‐Stokes’ drag law with a porosity scaled on a fractal geometry with coefficient a = 0.03 and D₃ = 1.4 (solid lines) and 1.8 (dashed lines). See the text for details on drag calculation

Reference